(This method works only at magnifications high enough to resolve features at the scale of an Airy pattern, eg., few microns.)
If the subject plane contains a point of light, the well-focused image created by perfect aberration-free lenses through a circular aperture is not a point but, due to unavoidable diffraction caused by finite apertures, an Airy pattern (a bright spot surrounded by concentric rings, as in the figure to the right).
With perfect lenses, the spacing between the Airy diffraction rings or bands is dependent only on the numerical aperture (NA) of the optical system and the wavelength of the light -- so by measuring the Airy ring spacing, we can determine NA. The larger NA (ie., the larger the aperture), the smaller the Airy disc and thus the sharper the image.
Usually the diffraction patterns mixed in with other light from the subject, or blend with diffraction patterns from neighbouring light sources into a blur -- both subtly reducing the quality of the image. However, if a particular point is much brighter than the surrounding area (ie., high contrast situations), the Airy diffraction rings are often visible when viewed at sufficiently high magnification.
When the lenses are not quite perfect (eg., have aberrations), the Airy pattern distorts and/or expands (reference).
In the photomicrograph below (figure 1) of an integrated circuit, a few of the surfaces happen to strongly reflect light into the stereomicroscope objective, creating what appear to be strong diffraction patterns that are visible where they spill into adjacent dark areas. The inset image in figure 1 shows the diffraction pattern at the pixel level. Green lines were placed by eye to mark the minima.

Fig 1. Integrated circuit, photographed with Canon A75 on a V434B stereomicroscope at 4.5x
The centers of the diffraction patterns in figure 1 are not obvious so the radius of the Airy disc cannot be measured directly. However, the ring minima are locatable, and have been marked with green lines in the inset figure of figure 1.
The first few minima of an aberration-free Airy pattern are at 3.83, 7.02, 10.17, and 13.33 'optical units' from its center (ref. Airy pattern), where a 'optical unit' is defined as:
1 Optical unit (OU) = λ / (2π NA), where λ is the wavelength of the light, and NA is the numerical aperture
Re-arranging for NA:
NA = λ / (2π OU)
The measured distances from the first Airy pattern minimum ring to the others (the green lines in the inset of figure 1) are in column D in the Excel spreadsheet fragment below. The corresponding distances, in optical units, from ring 1's minimum are in column C (eg., C6 = B6 - B4). The points are plotted on the right. We can use linear regression to find the number of sensor pixels per optical unit; the trend line, which passes through (0,0), shows the result. The Excel function for that (LINEST) is in cell B9; its formula is displayed at the top.
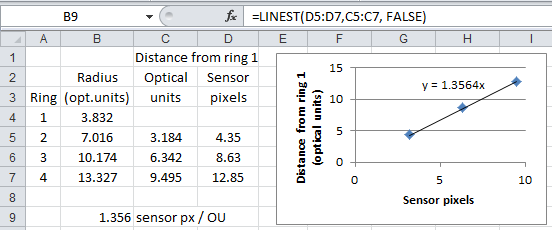
So one optical unit = 1.36 sensor pixels. Each sensor pixel corresponds to 1.030 μm in the subject plane (determined by photographng a 1 mm scale with the same microscope set-up), so that's (1.36)(1.03) = 1.40 μmsubjPlane/OU. Assuming λ = 550 nm (yellow-green) and aberration-free optics, we get:
NA = 550 nm / (2π 1.40) = 0.063
The Airy radius is 3.83 optical units (the distance to the first minimum). Given one optical unit is 1.40 μmsubjPlane (as measured using the A75), then:
rAiry = (3.83)(1.40) = 5.36 μmsubjPlane
By the Rayleigh Criterion, two points of light on the subject plane can be resolved if separated by more than the Airy distance, rAiry. But information is still available from subject plane objects that are smaller than rAiry, especially if they are isolated, or too dim to generate visible rings and a broad central peak, as can be assessed by looking at figure 1.
Figure 1 is a 100% crop, ie., actual pixels without scaling from a small part of a larger image. Figure 1's inset was created by zooming the image in Photoshop to make individual pixels visible (outlined by thin white lines in figure 1 inset), then doing a screen capture, and then analysing the captured image in Photoshop. This allows more precision when measuring distances.
Airy patterns discussed here are two-dimensional slices of three-dimensional 'point spread functions'. Focus and lens imperfections can create complications. But if you see nicely-formed Airy patterns in well-focused images using good quality optical equipment, I think the method above would likely produce reasonable results.
Here's a 2015 article that describes the observation and analysis of Airy patterns using a DSLR camera -- similar to the methods above and providing some confidence:
Kenneth Trantham and Timothy J. Reece, 2015. Demonstration of the Airy disk using photography and simple light sources. American Journal of Physics 83, 928 (2015); doi: 10.1119/1.4927525
2010-Dec: First issue
2016-Aug: HTML5, minor edits, added 'Links'